Современные компьютерные технологии предоставляют огромные возможности для развития процесса образования. Еще К. Д. Ушинский заметил: «Детская природа требует наглядности». Наглядность в математике - ключ к знаниям.
Очень важно с малых лет детей учить развивать воображение, которое будет помогать в дальнейшем изучению математики. История моделирования в математике прошла следующие этапы наглядности: моделирование геометрических тел с помощью бумаги, картона; папье-маше; геометрические тела из дерева, которые дети изготавливали на уроках труда. Модели из стекла, которые позволяли рассмотреть сечение тел и т. д.
В 2000 годах в школу пришло новое понятие — оригами. Оригами — древнее искусство складывания фигурок из бумаги. Если вы думаете, что это забава для детей, то очень глубоко ошибаетесь! Они помогают детям быстрее ориентироваться на плоскости и в пространстве; тренирует память и внимание; воспитывается целеустремлённость и сосредоточенность; развиваются воображение и творческие способности; элементы наглядно-образного и логического мышления, которые так нужны при изучении математики.
Каждый учитель, который сегодня работает в школе прошёл эти этапы моделирования реальной математики в жизни.
Но сегодня новое поколение детей, которое требует от учителя большего. Учитель должен идти в ногу со временем. Развитие науки и техники представляет новые возможности для совершенствования и использования современных средств обучения. Роль и место информационных технологий в современной школе неуклонно возрастают. К этому приводит необходимость создания более полного представления о них не только в рамках школьного курса информатики.
Компьютер обладает большими возможностями в реализации принципа наглядности на уроках математики, вызывает неизменный интерес. С его помощью можно изобразить плоские, объемные фигуры, предъявить фигуры в статичном и динамичном режиме. К компьютерным изображениям могут быть приложены определенные задания для выполнения их учащимися, что дает возможность отойти от обычной созерцательности и вовлечь учащихся в активную работу по изучению учебного материала.
SketchUp — простой, но мощный интерактивный инструмент трехмерного моделирования, с помощью которого можно опробовать и представить свои идеи в 3D-графике.Модель является понятием широким. Но основное его обозначение — упрощённое подобие предмета, явления, процесса и т.д., повторяющее свойства самого оригинала.
3D - моделирование, представляет прекрасную возможность не переводя бумагу и тем самым не губя деревья, увидеть свою модель в готовым виде.
Рассмотрим мотивацию деятельности детей на уроке математики.
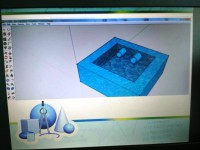
Задача: необходимо заполнить бассейн водой, с помощью труб разного диаметра…, этот тип задач в курсе математики можно встретить довольно часто при изучении обыкновенных дробей, задач на части, совместную работу и т.д. Если это построение выполнить в SketchUр, тем самым проиллюстрировать задачу из реальной математики в жизни, то у детей появиться желание: непременно решить её.
На рисунке изображена модель бассейна к задаче, выполненная в программе SketchUp. 
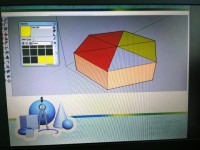
Моделирование частей, или частей целого при изучение сложения и вычитания дробей, можно также показать на примере торта, пирога, смоделировав 3D-модель в данном трёхмерном пространстве.
Офис настолько прост в обращении, яркая смена красок, поворот фигур, построение тел вращения — это только малая часть того, что мы можем получить от SketchUp на уроке.
Внедрение 3D моделирования, 3D-графики в математике обращено на достижение следующих целей: формирование познавательной активности учащихся; творческого мышления; опыта применения технологических знаний и умений в самостоятельной деятельности на практике. Как результат межпредметных связей математики и информатики: овладение умением строить трехмерные модели, изображать полученные результаты и только затем выполнять математические расчёты.
Компьютерное моделирование является одним из эффективных методов изучения сложных тем в курсе математики. Компьютерные модели проще и удобнее исследовать детям.
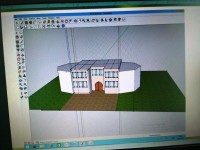
Проведение вычислительных экспериментов в точности и в тоже время трудности в реальной жизни, которые затрудняют расчёты из-за финансовых и физических препятствий, позволяют детям получить свой собственный опыт: познать себя дизайнером, архитектором, бухгалтером, инженером.
Эти приёмы мотивируют детей и повышают качество знаний учащихся по предмету.
Ссылка: https://cloud.mail.ru/public/4gKb/3xRVQQKnF
                                             Учитель математики и информатики Карагодина Н.Б. МБОУ "Некрасовская школа"